
Планиметрия
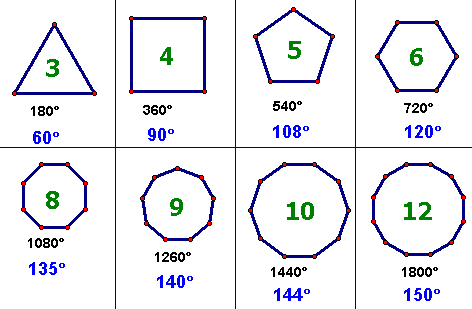
1. Правильный многоугольник — выпуклый многоугольник, у которого равны все стороны и все углы между смежными сторонами.
2. Признаки равенства треугольников.

3. Признаки равенства прямоугольных треугольников.

4. Равнобедренным называется треугольник,
у которого две стороны равны.

5. Признаки подобия треугольников.

6. Теорема Пифагора — в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

7. Тригонометрия.

8. Площадь треугольника.

9. Равносторонний треугольник-
треугольник, у которого все стороны равны.

10. Теорема Фалеса. Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
11. Обратная теорема Фалеса. Если на каждой стороне угла отложить от его вершины пропорциональные отрезки и через их концы провести прямые, то эти прямые параллельны друг другу.

12. Теорема косинусов.

13. Теорема синусов.
.jpg)
14. Диагональ квадрата равна стороне квадрата,
умноженной на корень из двух.

15. Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.

16. Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

17. Равнобедренная трапеция – трапеция, у которой боковые стороны равны.
.png)
18. Свойства параллелограмма.

19. Признаки параллелограмма.

20. Площадь прямоугольник.

21. Радиус, перпендикулярный хорде, делит эту хорду пополам.

22. Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.
23. Свойства средней линии треугольника.
1.Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.
2.Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.

24. Формулы площади и высоты равностороннего треугольника.
а - сторона треугольника.

25. Метод площадей — метод решения геометрических тождеств путём подсчёта площадей фигур разными способами.